Given a m * n matrix of ones and zeros, return how many square submatrices have all ones.
Example 1:
Input: matrix =
[
[0,1,1,1],
[1,1,1,1],
[0,1,1,1]
]
Output: 15
Explanation:
There are 10 squares of side 1.
There are 4 squares of side 2.
There is 1 square of side 3.
Total number of squares = 10 + 4 + 1 = 15.
Example 2:
Input: matrix =
[
[1,0,1],
[1,1,0],
[1,1,0]
]
Output: 7
Explanation:
There are 6 squares of side 1.
There is 1 square of side 2.
Total number of squares = 6 + 1 = 7.
Solution
Think of the dynamic programming technique.
Like what we did in Leetcode #221 Maximal Square, we had a dynamic programming approach to find the maximum side length of square for each matrix cell.
Similarly, this time, we can use same technique again.
First, find the max side length of square for each matrix cell by dynamic programming with optimal substructure (this will be described later).
Second, compute the summation of dynamic programming table, and we get the number of all square submatrices of given input matrix.
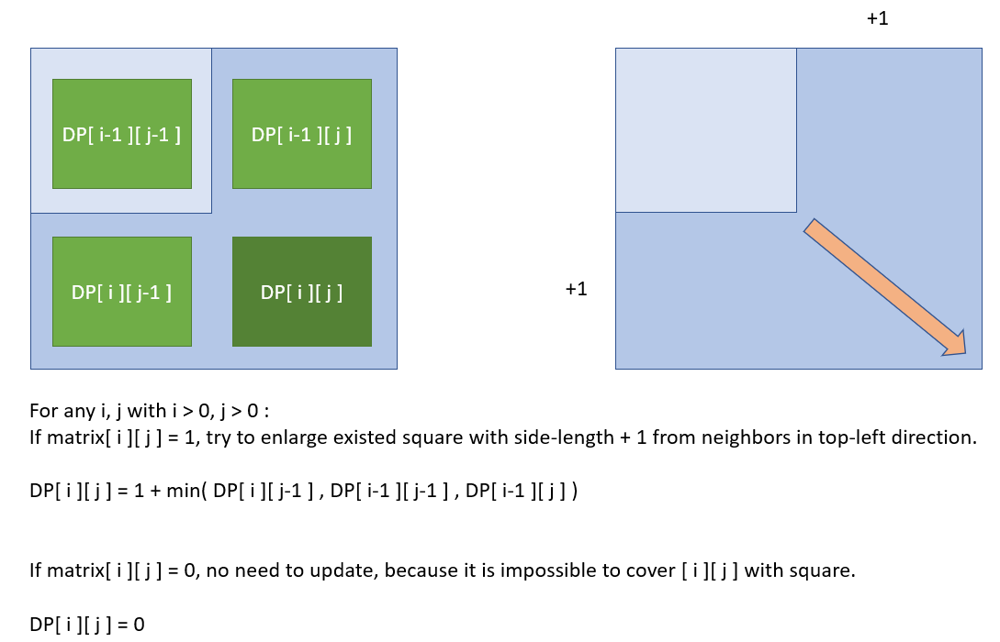
Optimal substructure: for maximum side length of square, in dynamic programming.
Let DP[ i ][ j ] denote the max side length, and [ *i* ][ *j* ] as the anchor point (i.e., bottom-right point) of square
For any i, j with i > 0 and j > 0: DP[ i ][ j ] = 1 + min( DP[ i ][ j - 1 ] , DP[ i - 1 ][ j - 1 ] , DP[ i ][ j - 1 ] ), if matrix[ i ][ j ] = 1
DP[ i ][ j ] = matrix[ i ][ j ] = 0, Otherwise.
Abstract model for update with optimal substructure:
class Solution:
def countSquares(self, matrix: List[List[int]]) -> int:
m = len(matrix)
n = len(matrix[0])
dp =[matrix[0][i] for i in range(n)]
res = sum(dp)
for i in range(1,m):
tmp = [matrix[i][0]]
for j in range(1,n):
if matrix[i][j]==1:
tmp.append(1 +min(tmp[-1],dp[j],dp[j-1]))
else:
tmp.append(0)
res +=sum(tmp)
dp=tmp[:]
return res